Infinite Rope Simulation

This idea was actually inspired by the Ludum Dare 47 theme “Stuck in a Loop”. I wanted to create a 2D platformer where the world was finite but you could move left or right forever and still find yourself in the same place. I thought it’d be interesting to have a simulated rope you could pull around the world that would wrap infinitely. I started with the infinite world (this is all done in Godot):

This works as follows: Each frame we calculate the left most tile coordinate relative to the player via:

func get_tile_offset():
	return floor(player.position.x / $TileMap.cell_size.x) - tiles_in_world / 2

Then we use this offset to determine how many tiles the player has moved since the last frame. For example, if the player has moved one tile in the positive direction (right) since the last frame then we need to take one vertical tile slice from the left and move it to the right. In reality I actually add 4 additional vertical slices to ensure there’s always tiles visible when moving quickly. The code for updating the tilemap is:

func update_tile_map(offset):
	# Determine the direction +ve right, -ve left
	var offset_change = offset - last_offset
	for i in range(abs(offset_change)):	
		# Get map slice we need to move
		var cells = []
		if sign(offset_change) > 0:
			cells = get_tile_map_slice(offset - i - 4)
		elif sign(offset_change) < 0:
			cells = get_tile_map_slice(offset + tiles_in_world + i + 4)
		# Up date the tilemap with the map slices
		for cell in cells:
			$TileMap.set_cell(cell.x + sign(offset_change) * (tiles_in_world), cell.y, 0, false, false, false, $TileMap.get_cell_autotile_coord(cell.x, cell.y))
			$TileMap.set_cell(cell.x, cell.y, -1, false, false, false, $TileMap.get_cell_autotile_coord(cell.x, cell.y))
			
	for i in range(4):
		# Get map slice we need to move
		var cells = []
		if sign(offset_change) > 0:
			cells = get_tile_map_slice(offset + i)
		elif sign(offset_change) < 0:
			cells = get_tile_map_slice(offset + tiles_in_world - i)
		# Up date the tilemap with the map slices
		for cell in cells:
			$TileMap.set_cell(cell.x + sign(offset_change) * (tiles_in_world), cell.y, 0, false, false, false, $TileMap.get_cell_autotile_coord(cell.x, cell.y))

Next I added gravity and a means to jump about.

The rope is simulated iteratively using Verlet integration. To get the simulation to work in this infinitely looping world, I store the rope node positions as if the world didn’t wrap then convert it back to a screen position after the rope physics has been calculated. The formulas for this conversion are below. For each rope node:

# If node is off the screen then wrap it back around.
# Calc node position as if world didn't wrap
nodes[i].pos = nodes[i].global_position + nodes[i].x_offset * world.world_size
# Calc distance from player (left -ve right +ve)
var diff = (nodes[i].pos.x) - player.position.x
# Calc "number of wraps"
nodes[i].x_offset.x = int((diff + sign(diff) * world.world_size / 2) / (world.world_size))
# Wrap pos to position on screen. 
nodes[i].global_position = nodes[i].pos - nodes[i].x_offset * world.world_size

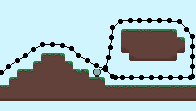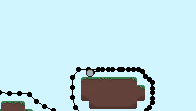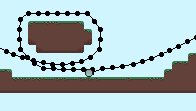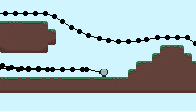
Where pos is the world position and global_position is the screen position. Below shows the x_offset for each node. This corresponds to the number of wraps the node has undergone and is used to convert between world and screen positions.

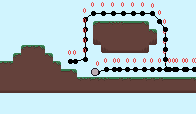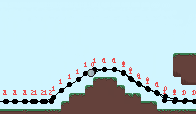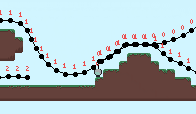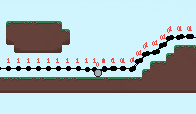
It’s pretty costly to do these rope simulations, especially with collisions, but I think the effect is pretty neat. The code is available on Github.